概率论和信息论
- 基本概念
贝叶斯准则:在已知P(y|x)和P(x)的情况下,$P(x|y) = \frac{p(x)P(y|x)}{P(y)}$, 贝叶斯准则经常被用在已知参数的先验分布情况下求后验分布。
信息熵:描述某个概率分布之间的相似度的度量。记做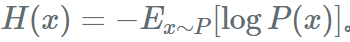
交叉熵:描述两个概率分布之间的相似度的指标,在机器学习中使用它作为分类任务的损失函数。记做: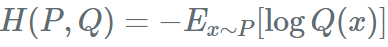
- 常见分布
伯努利二元分布
Multinoulli分布
高斯分布
拉普拉斯分布:有着和高斯分布很相近的形式,概率密度为: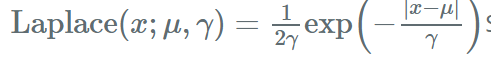
常用函数:
Logistics sigmoid函数
ReLU函数
Softplus函数:
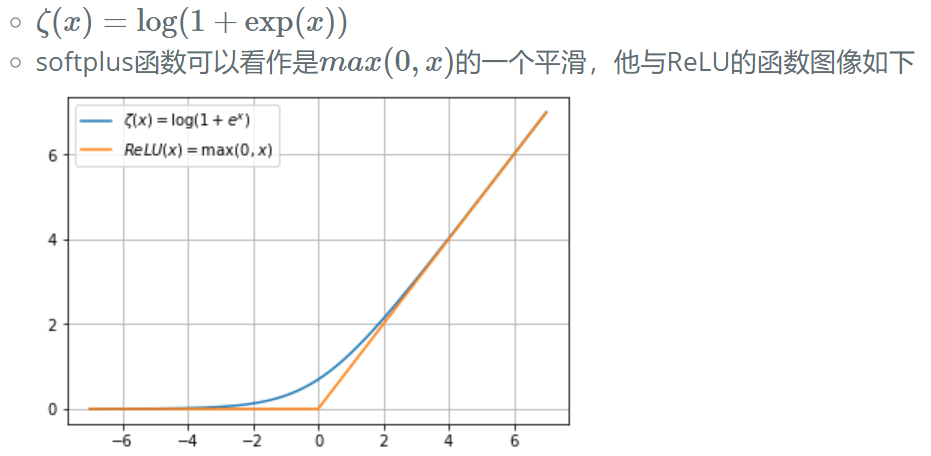
- 结构化概率模型:
概率图模型:使用图的概念来表示概念之间的概率依赖关系,下面就是关于a,b,c,d,e之间的有向图模型,通过该图可以计算:
$$ P(a,b, c, d, e) = p(a)p(b|a)p(c|a,b)p(d|b)p(e|c)$$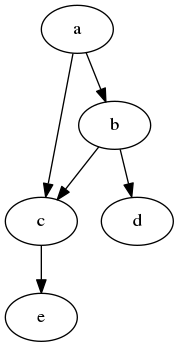
机器学习基础
性能度量
- 准确率
- 错误率
- 精度
- 召回率
- F1值
容量、过拟合和欠拟合
泛化能力是模型在未知数据上的表现是否良好。通常情况下,机器学习的模型是要作用在未知的数据上的,具有良好泛化能力的模型才是符合需求的。
训练误差
测试误差
欠拟合
过拟合:模型在训练集和测试集上的误差差距过大,通常由于模型过分拟合了训练集中的随机噪音,导致泛化能力较差。
最大似然估计
在已知分布的样本上,但是不知道分布的具体参数的情况下,根据样本值推断最有可能产生样本的参数值。
最大似然估计的一种解释是使$p_{model}$和$p_{data}$之间的差异性尽可能的小,形式化的描述为最小化两者的KL散度。