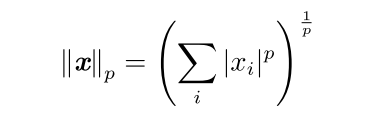内容来自:https://github.com/elviswf/DeepLearningBookQA_cn
1. 列举常见的一些范数及其应用场景,如 L0,L1,L2,L∞,Frobenius 范数
平方范数$L^2$对每个元素的导数和整个向量相关,所以在原点附近增长的非常的缓慢,在机器学习应用中,区分0和非零的元素非常重要。L1范数可以保证各个位置的斜率相同,同时保持简单的数学形式。
最大范数: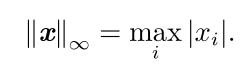
Frobenius范数表示矩阵的大小,类似于矩阵的L2范数。
L1范数&L2范数
L1正则化会产生稀疏解,L2正则化会使得权值趋向于0但是不等于0.
原因:L1范数在任意位置的导数都是相同的,权值是朝着0的位置缩减,衰减步长不变,权值很容易就会衰减到0.
L2范数在某个位置的导数和整个向量的位置有关,衰减的步长是和位置成正比的,所以越接近0的位置衰减越慢,权值会趋近于0但是不会等于0.
正则化的原理
首先,模型出现过拟合原因是训练数据中有噪音,模型过度拟合这些噪音数据导致学习到的模型泛化能力差。正则化是通过对参数的大小进行惩罚,限制模型的参数空间,从而减少了模型的有效容量,抑制拟合噪音的能力,从而提高泛化能力。
简单介绍一下贝叶斯概率与频率派概率,以及在统计中对于真实参数的假设。
频率学派,其特征是把需要推断的参数θ视作固定且未知的常数,而样本X是随机的,其着眼点在样本空间,有关的概率计算都是针对X的分布。另一派叫做贝叶斯学派,他们把参数θ视作随机变量,而样本X是固定的,其着眼点在参数空间,重视参数θ的分布,固定的操作模式是通过参数的先验分布结合样本信息得到参数的后验分布。
作者:秦松雄
链接:https://www.zhihu.com/question/20587681/answer/23060072
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
概率密度的万能近似器
高斯混合模型是概率密度的万能近似器,任何平滑的概率密度都可以用具有足够多组建的高斯混合模型以任意精度逼近。
简单介绍一下 sigmoid,relu,softplus,tanh,RBF 及其应用场景
- sigmoid函数用阿里产生Bernoulili分布的参数,在变量取绝对值非常大的时候,会出现饱和情况,函数会变得很平。
- softplus函数:$f(x) = log(1 + exp(x))$
- Relu函数:计算及其简单,在非零位置求导很快。不需要复杂的运算。
缓解了梯度消失的问题;
缺点:如果初始化或者learning rate设置的不好,会导致神经元die的问题。
5.Jacobian,Hessian 矩阵及其在深度学习中的重要性
答:p56-p62
Jacobian是一阶的偏导。
Hessian矩阵是二阶的偏导。二阶导数可以告诉我们一阶导数是怎么进行变化的。
Hessian矩阵可以确定一个临界点是否是局部极大点,全局极小点或者是鞍点。
正定是全局极小点,负定是局部极大点,有负有正是鞍点。
6.KL 散度在信息论中度量的是那个直观量
答:p46
KL散度用来衡量两个单独的概率分布的差异(信息熵的差值)
和KL散度密切相关的是交叉熵。交叉熵是计算在样本的真实分布的前提下,预测样本分布的信息熵。
等价于KL 散度,因为真实样本分布是确定的。
7. 数值计算中的计算上溢与下溢问题,如 softmax 中的处理方式
答:p52-p53
上溢出是计算的数值过大。
下溢出是接近于0的时候,因为四舍五入为0,一般会设置一个eps,保证不为0.
减去最大值。
softmax(x) = (exp(x - max(x)))/ sum(exp(x_i - max(x)))
8. 与矩阵的特征值相关联的条件数 (病态条件) 指什么,与梯度爆炸与梯度弥散的关系
答:p53;
输入被轻微扰动,输出就发生了很大变化的情况。
9. 在基于梯度的优化问题中,如何判断一个梯度为 0 的零界点为局部极大值/全局极小值还是鞍点,Hessian 矩阵的条件数与梯度下降法的关系
答:p56-p62
Hessian矩阵在局部极小点只有正特征值,在鞍点,同时具有正负特征值。
10.KTT 方法与约束优化问题,活跃约束的定义
答:p60-p61
11. 模型容量,表示容量,有效容量,最优容量概念
答:p70;p71;p72
12. 正则化中的权重衰减与加入先验知识在某些条件下的等价性
答:p73
13. 高斯分布的广泛应用的缘由
答:p40
14. 最大似然估计中最小化 KL 散度与最小化分布之间的交叉熵的关系
答:p84
15. 在线性回归问题,具有高斯先验权重的 MAP 贝叶斯推断与权重衰减的关系,与正则化的关系
答: p87
16. 稀疏表示,低维表示,独立表示
答:p92
17. 列举一些无法基于地图 (梯度?) 的优化来最小化的代价函数及其具有的特点
答:p97 维度灾难
18. 在深度神经网络中,引入了隐藏层,放弃了训练问题的凸性,其意义何在
答:p119-122
19. 函数在某个区间的饱和与平滑性对基于梯度的学习的影响
答:p98
20. 梯度爆炸的一些解决办法
答:p185
21.MLP 的万能近似性质
答:p123
22. 在前馈网络中,深度与宽度的关系及表示能力的差异
答:p125
23. 为什么交叉熵损失可以提高具有 sigmoid 和 softmax 输出的模型的性能,而使用均方误差损失则会存在很多问题。分段线性隐藏层代替 sigmoid 的利弊
答:p140
24. 表示学习的发展的初衷?并介绍其典型例子: 自编码器
答:p3
25. 在做正则化过程中,为什么只对权重做正则惩罚,而不对偏置做权重惩罚
答:p142
26. 在深度学习神经网络中,所有的层中考虑使用相同的权重衰减的利弊
答:p142
27. 正则化过程中,权重衰减与 Hessian 矩阵中特征值的一些关系,以及与梯度弥散,梯度爆炸的关系
答:p142-144
28.L1/L2 正则化与高斯先验/对数先验的 MAP 贝叶斯推断的关系
答:p144
29. 什么是欠约束,为什么大多数的正则化可以使欠约束下的欠定问题在迭代过程中收敛
答:p147 页底 Chapter 7.3
30. 为什么考虑在模型训练时对输入 (隐藏单元/权重) 添加方差较小的噪声,与正则化的关系
答:p149-p150 Chapter 7.5-7.6
31. 共享参数的概念及在深度学习中的广泛影响
答:多任务学习 p151;p156 Chapter 7.7; 7.9
32. Dropout 与 Bagging 集成方法的关系,以及 Dropout 带来的意义与其强大的原因
答:p159-p165 Chapter 7.12
33. 批量梯度下降法更新过程中,批量的大小与各种更新的稳定性关系
答:p170 Chapter 8.1.3
34. 如何避免深度学习中的病态,鞍点,梯度爆炸,梯度弥散
答:p173-p178 Chapter 8.2.1
35.SGD 以及学习率的选择方法,带动量的 SGD 对于 Hessian 矩阵病态条件及随机梯度方差的影响
答:p180;p181-p184 Chapter 8.3;
36. 初始化权重过程中,权重大小在各种网络结构中的影响,以及一些初始化的方法;偏置的初始化
答:初始化权重:p184; Chapter 8.4
偏置初始化:p186页底 Chapter 8.4
37. 自适应学习率算法: AdaGrad,RMSProp,Adam 等算法的做法
答:AdaGrad:p187;
RMSProp:p188;
Adam:p189 Chapter 8.5.1-3
38. 二阶近似方法: 牛顿法,共轭梯度,BFGS 等的做法
答:牛顿法:p190 Chapter 8.6.1;
共轭梯度: p191-p193; Chapter 8.6.2
BFGS:p193-p194 Chapter 8.6.3
39.Hessian 的标准化对于高阶优化算法的意义
答:p195 Chapter 8.7.1
40. 卷积网络中的平移等变性的原因,常见的一些卷积形式
答:平移等变性:p205页底; Chapter 9.3
常见的一些卷积形式:p211-p218 Chapter 9.5
41.pooling 的做法的意义
答:p207; p210 Chapter 9.3-4
42. 循环神经网络常见的一些依赖循环关系,常见的一些输入输出,以及对应的应用场景
答:p230-p238 Chapter 10.2
43. seq2seq,gru,lstm 等相关的原理
答:seq2seq:p240-p241; Chapter 10.4
gru:p250; Chapter 10.10.2
lstm:p248 Chapter 10.10.1
44. 采样在深度学习中的意义
答:p286 第一段 Chapter 12.4.3
45. 自编码器与线性因子模型,PCA,ICA 等的关系
答:线性因子模型可以扩展到自编码器和深度概率模型: p304-p305; Chapter 13.5
PCA:p298; Chapter 13.1
ICA:p298 Chapter 13.2
46. 自编码器在深度学习中的意义,以及一些常见的变形与应用
答:意义: p306 Chapter 14.1
常见变形: p306-p313 Chapter 14.5
应用: p319 Chapter 14.9
47. 受限玻尔兹曼机广泛应用的原因
答:p400: 想特别了解的人注意这句话: See Mohamed et al. (2012b) for an analysis of reasons for the success of these models. Chapter 20.2
48. 稳定分布与马尔可夫链
答:p362 Chapter 17.3
49.Gibbs 采样的原理
答:p365 Chapter 17.4
50. 配分函数通常难以计算的解决方案
答:p368 Chapter 17.5.2
“遇到难以处理的无向图模型中的配分函数时, 蒙特卡洛方法仍是最主要工具”
51. 几种参数估计的联系与区别: MLE/MAP/贝叶斯
答:P82/85/87 Chapter 5.5
52. 半监督的思想以及在深度学习中的应用
答:p329-p332 Chapter 15.3
53. 举例 CNN 中的 channel 在不同数据源中的含义
答:p219-220 Chapter 9.7
54. 深度学习在 NLP,语音,图像等领域的应用及常用的一些模型
答:p272-p293 Chapter 12.1-5
55.word2vec 与 glove 的比较
答:How is GloVe different from word2vec?;
GloVe 以及 Word2vec 能称为 deep learning 么?这俩模型的层次其实很浅的;
这个问题没找到答案,我去找了 quora 和知乎上的相关问题以及 quora 一个回答提及的论文。 (若有人在书中找到,请批评指正)
56. 注意力机制在深度学习的某些场景中为何会被大量使用,其几种不同的情形
答:p288 Chapter 12.4.5.1
57.wide&deep 模型中的 wide 和 deep 介绍
答:https://arxiv.org/pdf/1606.07792.pdf#### 此问题答案未在书中找到,为此我去找了原论文,论文图 1 有详细的介绍。 (若有人在书中找到,请批评指正)
58. 核回归与 RBF 网络的关系
答:p89 Chapter 5.7.2
59.LSTM 结构推导,为什么比 RNN 好?
答:p248 Chapter 10.10
60. 过拟合在深度学习中的常见的一些解决方案或结构设计
答:p143-159; Chapter 7.1-12
包括:Parameter Norm Penalties(参数范数惩罚); Dataset Augmentation (数据集增强); Early Stopping(提前终止); Parameter Tying and Parameter Sharing (参数绑定与参数共享); Bagging and Other Ensemble Methods(Bagging 和其他集成方法);Dropout. 另外还有 Batch Normalization。
61. 怎么理解贝叶斯模型的有效参数数据会根据数据集的规模自动调整
答:关于非参数模型:p72 ; Chapter 5.2
非参数模型不依赖于特定的概率模型,它的参数是无穷维的,数据集的规模的大小影响着模型使用更多或者更少的参数来对其进行建模。(并未在书中找到准确的答案,若有更好的回答,请联系我改正)
本答案是根据问题在Deep Learning上找到的答案;有些答案只是自己读书后在书上做的笔记的具体页面,毕竟原 po(http://t.cn/RObdPGk) 说还有另外一本书,所以该答案可能不是特别准确也不完善,答案也是给大家做个参考,若发现答案有问题,请联系我并指正,大家共同进步,谢谢!